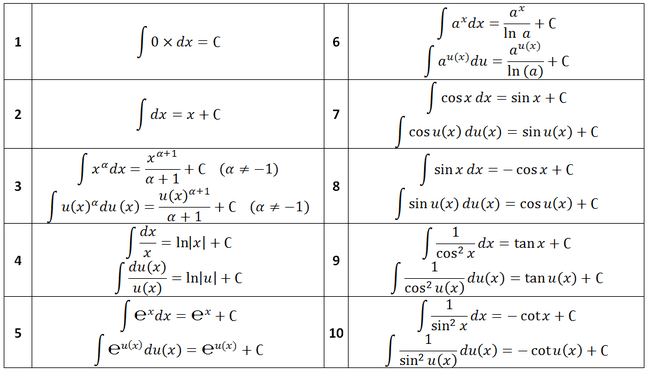Định nghĩa tích phân là một khái niệm cốt lõi trong toán học, đóng vai trò quan trọng trong việc tính toán diện tích, thể tích, và nhiều ứng dụng khác. Bằng cách sử dụng tích phân, chúng ta có thể giải quyết các bài toán liên quan đến tốc độ biến thiên của hàm số, xác định tổng lượng thông qua một quá trình không liên tục, và nắm bắt những khía cạnh sâu sắc về các sự biến đổi trong toán học và khoa học tự nhiên.
Định nghĩa đơn giản của tích phân
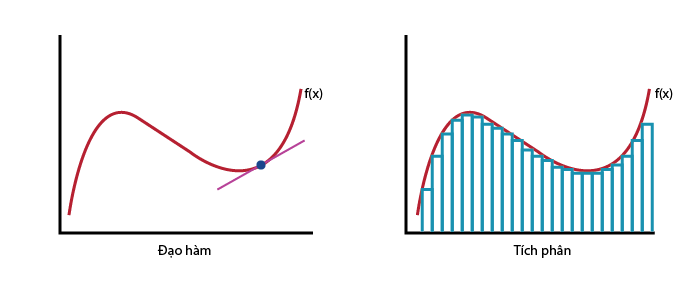
Tích phân là một phép tính được sử dụng để tìm ra diện tích dưới đường cong của một đồ thị hoặc giá trị tổng quát của một hàm số trong một khoảng xác định. Chúng ta thường sử dụng ký hiệu “∫” để biểu diễn phép tích phân và gọi nó là “đạo hàm ngược”. Một khái niệm quan trọng khác liên quan đến tích phân là định nghĩa riêng của hàm số trong một khoảng xác định, được gọi là “nguyên hàm”.
Tích phân và diện tích

Một ứng dụng cơ bản của tích phân liên quan đến việc tính toán diện tích. Khi chúng ta có một đường cong trên mặt phẳng, chúng ta có thể sử dụng tích phân để tìm diện tích dưới đường cong đó. Ví dụ, để tính diện tích hình chữ nhật với chiều rộng là a và chiều cao là b, ta sử dụng công thức Diện tích = a * b. Tuy nhiên, khi chúng ta muốn tính diện tích của các hình dạng phức tạp hơn, chẳng hạn như hình tròn hoặc elip, tích phân trở thành công cụ hữu ích.
Tích phân và biểu thức toán học
Tích phân không chỉ giúp chúng ta tính toán diện tích mà còn là một công cụ mạnh mẽ trong việc tìm giá trị tổng quát của một hàm số trong một khoảng xác định. Chúng ta có thể sử dụng tích phân để tính toán trung bình của một hàm số trong một khoảng, tìm ra các giá trị tối đa và tối thiểu của một hàm số, hay thậm chí tính toán khối lượng của một vật thể không đều.
Tích phân và ứng dụng trong khoa học tự nhiên
Tích phân không chỉ có ý nghĩa trong toán học thuần túy, mà còn được áp dụng rộng rãi trong các lĩnh vực khoa học tự nhiên như vật lý, hoá học, và kỹ thuật. Ví dụ, trong vật lý, tích phân được sử dụng để tính toán lực đẩy, quãng đường di chuyển, và năng lượng tiêu thụ.## Tích phân và ứng dụng trong vật lý
Trong lĩnh vực vật lý, tích phân đóng vai trò quan trọng trong việc tính toán các đại lượng vật lý quan trọng như khối lượng, trọng lực, động năng, công suất và nhiệt lượng. Chẳng hạn, khi ta muốn tính khối lượng của một vật thể không đều, chúng ta có thể sử dụng tích phân để tính diện tích xuyên qua vật thể và nhân với mật độ khối lượng tại từng điểm trong vật thể đó.
Ngoài ra, trong lĩnh vực cơ học, tích phân cũng được sử dụng để tính địa chỉ trung bình của một hệ thống hạt và giúp chúng ta hiểu sâu hơn về chuyển động và tương tác giữa các hạt trong một hệ thống.
Tích phân và ứng dụng trong kỹ thuật

Trong kỹ thuật, tích phân là một trong những công cụ quan trọng để giải quyết các vấn đề liên quan đến thiết kế, xây dựng và phân tích các hệ thống phức tạp. Ví dụ, trong ngành kỹ thuật cơ khí, tích phân được sử dụng để tính toán độ chính xác của các bộ phận máy móc, tính toán tải trọng và độ bền của vật liệu, hay tính toán hiệu suất của các hệ thống điện và điện tử.
Tích phân cũng được ứng dụng rộng rãi trong kỹ thuật xây dựng và kiến trúc. Chẳng hạn, để tính toán diện tích xây dựng, diện tích mặt bằng hoặc tính toán lượng vật liệu cần thiết cho việc xây dựng, tích phân là công cụ không thể thiếu.
Tích phân và ứng dụng trong khoa học xã hội
Ngoài các lĩnh vực khoa học tự nhiên, tích phân cũng có ứng dụng trong khoa học xã hội như kinh tế học, ngành y học, xã hội học và thống kê. Ví dụ, trong kinh tế học, tích phân được sử dụng để tính toán sản lượng quốc gia, dự báo tăng trưởng kinh tế và phân tích chính sách kinh tế.
Trong y học, tích phân được sử dụng để tính toán diện tích dưới đường cong của đồ thị chuẩn đoán bệnh và tính toán diện tích dưới đường cong của đồ thị thuốc. Điều này giúp bác sĩ và nhà nghiên cứu phân tích kết quả và hiệu quả của các liệu pháp điều trị.
Kết luận
Tích phân là một công cụ hữu ích trong toán học và được ứng dụng rộng rãi trong nhiều lĩnh vực khoa học và kỹ thuật. Từ việc tính toán diện tích đơn giản đến phân tích sự biến thiên của các hàm số phức tạp, tích phân cho phép chúng ta khám phá và hiểu sâu hơn về các quy luật tựtự tổ chức trong tự nhiên và xã hội. Qua việc áp dụng tích phân, chúng ta có thể giải quyết các bài toán thực tế và tạo ra những ứng dụng hữu ích.
Từ những khái niệm cơ bản về tích phân đến ứng dụng của nó trong các lĩnh vực khác nhau, chúng ta đã thấy rằng tích phân là một công cụ mạnh mẽ và linh hoạt. Nó không chỉ cho phép chúng ta tính toán diện tích và giá trị tổng quát của hàm số mà còn mang lại sự hiểu biết sâu sắc về sự biến thiên và tương tác trong các quy luật tự nhiên và xã hội.
Với sự phát triển của công nghệ và ứng dụng của tích phân, chúng ta có thể tiếp tục khám phá và tìm hiểu thêm về các phương pháp tích phân mới và cách chúng có thể được áp dụng để giải quyết các vấn đề phức tạp. Định nghĩa tích phân đã tạo nên nền tảng cho sự phát triển toán học và khoa học tự nhiên, đồng thời mang lại những lợi ích và ứng dụng sâu rộng trong cuộc sống hàng ngày của chúng ta.
- Kem chống nắng Super Perfect The Face Shop review sản phẩm hot nhất
- Review: Nên dùng máy ép trái cây tốc độ nhanh hay tốc độ chậm?
- Nhà Nhập Khẩu Và Phân Phối Rejuvaskin Việt Nam Thông Báo Thay Đổi Tem Chống Hàng Giả Mới
- Sinh năm 1984 là tuổi gì? Tử vi tuổi Giáp Tý (1984) nam, nữ mạng
- Kỳ lạ về hai người đàn bà chuyển nhượng chồng với giá 50 triệu đồng
- Giải mã giấc mơ thấy thỏ